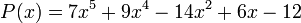Explicacion con nuestras Propias palabras

Espero que puedan entender esto. Es hecho con mucho esmero para Uds. Thank you.


Algebra: Monomios y Polinomios Parte II
View more documents from kik3z.



Algebra: Monomios y Polinomios Parte III
View more documents from kik3z.



bueno la Parte I esta en proceso debido a unos errores de sistema
gracias por su comprension.
1 comentario:

Concepto del Polinomio y Monomio

Empezemos con el monomio:
Un monomio es una expresión algebraica en la que se utilizan letras, números y signos de operaciones. Las únicas operaciones que aparecen entre las letras son el producto y la potencia de exponente natural. Se denomina polinomio a la suma de varios monomios. Un monomio es un polinomio con un único término.

Elementos de un monomio

Un monomio posee una serie de elementos con denominación propia.

Dado el monomio 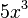5x^3 \;, se distinguen los siguientes elementos:



El coeficiente de un monomio es el número que aparece multiplicando a la parte literal. Normalmente se coloca al principio. Si tiene valor 1 no se escribe, y nunca puede ser cero ya que la expresión completa tendría valor cero.

Si un monomio carece de coeficiente, este equivale a uno.
Si algún término carece de exponente, este es igual a uno.
Si alguna parte literal no está presente, pero se requiere, entonces se considera con exponente cero, ya que: \forall x \in \mathbf{R}: x^{0} = 1 \,

Dada una variable 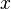x \;, un número natural 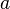a \; y un número real \alpha \; la expresión \alpha \cdot x^a =\alpha x^a \, es un monomio.

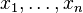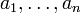Si tenemos varias variables: x_1,\ldots,x_n, el número real \alpha \; y los números naturales a_1,\ldots,a_n \,, el producto correspondiente 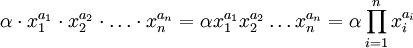\alpha \cdot x_1^{a_1}\cdot x_2^{a_2}\cdot\ldots \cdot x_n^{a_n} = \alpha x_1^{a_1} x_2^{a_2}\ldots x_n^{a_n} =\alpha \prod_{i=1}^{n}x_{i}^{a_{i}}\, también es un monomio.

Grado de un monomio

El grado de un monomio es igual a la suma de los exponentes de las variables que lo componen.

Ejemplos
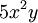5x^2 y \; tiene grado 3
pues equivale a la expresión: 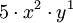5\cdot x^2 \cdot y^1 \; y la suma de los exponentes es 2 + 1 = 3
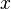x \; tiene grado 1
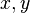pues equivale a 1x^1 \; y respecto de x, y\; a la expresión: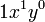 1x^1 y^0 \;
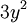3y^2 \; tiene grado 2
y equivale respecto de 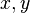x, y\; a la expresión: 1x^0 3y^2 \;

En matemática se considera que el número cero es un monomio de grado “menos infinito” con el fin de que se respete la regla de que el grado del producto de los monomios es igual a la suma de los grados de los factores.


Ahora el Polinomio:

Polinomio, en matemáticas, se denomina a la suma de varios monomios, llamados términos del polinomio. Es una expresión algebraica constituida por una o más variables, utilizando solamente operaciones de adición, sustracción, multiplicación y exponentes numéricos positivos. El polinomio de un sólo término se denomina monomio, el de dos binomio, el de tres trinomio.

La expresión general de los polinomios que sólo tienen una variable, los más utilizados, es:

P(x)= a_n x^{n} + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_2 x^2 + a_1 x + a_0 \,

por ejemplo:

P(x)= 7 x^5 + 9 x^4 - 14 x^2 + 6 x - 12 \,

Se denomina grado de un polinomio a la mayor potencia de los monomios que lo componen.


Definición algebraica

Para a0, …, an constantes en algún anillo (en particular podemos tomar un cuerpo, como \mathbb{R} o \mathbb{C}, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma

P(x) = a_n x^n + a_{n - 1} x^{n - 1}+ \cdots + a_1 x^{1} + a_0 x^{0}.

El polinomio se puede escribir más concisamente usando sumatorios como

P(x) = \sum_{i = 0}^{n} a_{i} x^{i}.

Las constantes a0, …, an se llaman los coeficientes del polinomio. A a0 se le llama el coeficiente constante (o término independiente) y a an, el coeficiente principal. Cuando el coeficiente principal es 1, al polinomio se le llama mónico o normado. Siendo x un símbolo llamado indeterminada.

40 comentarios:

Seguimos con la Introduccion al Polinomio y Binomio

1.04 Polinomios



Polinomios
No hay comentarios:

Introduccion al Polinomio y Monomio

No hay comentarios:

Presentación

El presente módulo de Matemática para el tercer grado de educación secundaria se ha estructurado de acuerdo a los contenidos y capacidades de nuevo programa oficial vigente.
Los temas son presentados con claridad y sencillez usando el leguaje adecuado y los sí…mbolos correspondientes. Los ejercicios considerados en este texto, han sido elaborados cuidadosamente, teniendo en cuenta el grado de dificultad que va de menor a mayor.
Este modulo de aprendizaje es de la forma siguiente:
1°† UNIDAD DE EXPRESIONES ALGEBRAICAS, que considera polinomios en R, operaciones con polinomios, productos notables y cocientes notables, factorización y racionalización.
2†° UNIDAD DE RELCIONES Y FUNCIONES, que comprende:
Relaciones: conceptos de relación binaria, dominio, rango, propiedades, relación de equivalencia y relación de orden.
A fin de alcanzar las capacidades esperadas. Se deben trabajar minuciosamente todas y cada una de las actividades del presente módulo, asimismo cada alumno será evaluado y autoevaluado, recomendándole un permanente esp…ritu de honradez para responder, pues de ello depende el logro de un aprendizaje satisfactorio. El alumno, tendrá la oportunidad de chequear sus aciertos y errores en la hoja de respuestas y aclarando sus dudas alo que denominamos solucionario que se da al término de todas las actividades
y unidades.
No hay comentarios:
Suscribirse a: Entradas (Atom)