Elementos de un monomio
Un monomio posee una serie de elementos con denominación propia.
Dado el monomio 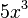 , se distinguen los siguientes elementos:
, se distinguen los siguientes elementos:
- coeficiente:

- parte literal:

El coeficiente de un monomio es el número que aparece multiplicando a la parte literal. Normalmente se coloca al principio. Si tiene valor 1 no se escribe, y nunca puede ser cero ya que la expresión completa tendría valor cero.
- Si un monomio carece de coeficiente, este equivale a uno.
- Si algún término carece de exponente, este es igual a uno.
- Si alguna parte literal no está presente, pero se requiere, entonces se considera con exponente cero, ya que:

Dada una variable 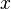 , un número natural
, un número natural 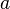 y un número real
y un número real  la expresión
la expresión  es un monomio.
es un monomio.
Si tenemos varias variables: 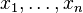 , el número real
, el número real  y los números naturales
y los números naturales 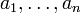 , el producto correspondiente
, el producto correspondiente 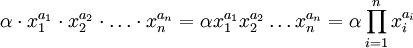 también es un monomio.
también es un monomio.
Grado de un monomio
El grado de un monomio es igual a la suma de los exponentes de las variables que lo componen.
- Ejemplos
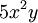 tiene grado 3
tiene grado 3 -
- pues equivale a la expresión:
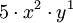 y la suma de los exponentes es 2 + 1 = 3
y la suma de los exponentes es 2 + 1 = 3
- pues equivale a la expresión:
-
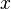 tiene grado 1
tiene grado 1 -
- pues equivale a
 y respecto de
y respecto de 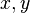 a la expresión:
a la expresión: 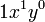
- pues equivale a
-
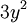 tiene grado 2
tiene grado 2 -
- y equivale respecto de
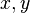 a la expresión:
a la expresión: 
- y equivale respecto de
-
En matemática se considera que el número cero es un monomio de grado “menos infinito” con el fin de que se respete la regla de que el grado del producto de los monomios es igual a la suma de los grados de los factores.
Ahora el Polinomio:
Polinomio, en matemáticas, se denomina a la suma de varios monomios, llamados términos del polinomio. Es una expresión algebraica constituida por una o más variables, utilizando solamente operaciones de adición, sustracción, multiplicación y exponentes numéricos positivos. El polinomio de un sólo término se denomina monomio, el de dos binomio, el de tres trinomio.
La expresión general de los polinomios que sólo tienen una variable, los más utilizados, es:
por ejemplo:
Se denomina grado de un polinomio a la mayor potencia de los monomios que lo componen.
Definición algebraica
Para a0, …, an constantes en algún anillo (en particular podemos tomar un cuerpo, como  o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma
El polinomio se puede escribir más concisamente usando sumatorios como
Las constantes a0, …, an se llaman los coeficientes del polinomio. A a0 se le llama el coeficiente constante (o término independiente) y a an, el coeficiente principal. Cuando el coeficiente principal es 1, al polinomio se le llama mónico o normado. Siendo x un símbolo llamado indeterminada.

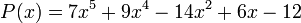




eso es mate necesito la descripcion del polinomio pero en definicon algebraica
ResponderEliminarFelicito el resumen sencillo de los terminos ya que facilitarán la compresión a los que sí se interesan en la materia
ResponderEliminarEste comentario ha sido eliminado por el autor.
Eliminarcomo tu madre caga XDDDD
EliminarEsto no me sirve
EliminarFacil de entender
ResponderEliminarFacil de entender
ResponderEliminarllupamela poronga
EliminarAndá a estudiar analfabeto!!
EliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarFacil de entender me gusta
ResponderEliminarjajajajaja
ResponderEliminar15646512516541
ResponderEliminar1478895216485
ResponderEliminar111l5ñ32
ResponderEliminargracias por hacer este trabajo me es muy util
ResponderEliminarIncreible entendi perfectamente el polinomio muchas gracias juasjuasjuasjuasjuas
ResponderEliminarGracias, nuevamente me gustan las matematicas
ResponderEliminaresta muy bien explicados
ResponderEliminaresta bueno
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarlo entiendo muy bien
ResponderEliminarEsta muy bien
ResponderEliminarMuy bien explicado y fácil de entender. Gracias.
ResponderEliminarMuy satisfactible ya entiendo todo
ResponderEliminarsolo los burros vinieron a saber que eraa :v
ResponderEliminarno loentiendo
ResponderEliminarMuy bueno esto esta bien explicado y con interes a las matemáticas👏👏👏👏👏👏👏👏🖒
ResponderEliminarmuy bueno
ResponderEliminarComo hacer para sumar px +qx
ResponderEliminarme sirvio de mucho
ResponderEliminarGracias es muy útil
ResponderEliminarGracias es muy útil
ResponderEliminarCallate la boca no dice un coño esto
ResponderEliminarconoceis a rosAMELANO
ResponderEliminarQUE ME LA AGARRA CON LAS DOS MANANOS XDXDXDXDXDX
ResponderEliminar.
ResponderEliminar훌륭하지만이 주소의 데이터를 살펴보십시오. 먹튀검증
ResponderEliminarI have bookmarked it and I am anticipating perusing new articles. Keep doing awesome 먹튀폴리스
ResponderEliminarLa verdad no lo entiendo
ResponderEliminar